摘要：我国当前正面临的低生育率、老龄化等人口发展问题，给社会经济各方面带来了前所未有的压力。而房地产市场中房价的波动一直都是各界人士关注的热门话题，其关乎着经济可持续发展和社会稳定。厘清区域人口结构变化对其商品房价格的影响有助于科学解释房价变动因素，进而准确预测房价走势。因此该文基于人口构成理论，从人口自然结构、人口社会结构、人口地域结构三方面选取指标，借助SPSS软件进行多因素回归的实证分析，探讨人口结构变化对重庆市商品房价格的影响，并提出相应建议以期维护其房地产行业的稳定。

关键词： 人口结构;重庆市;房地产价格

1 引言

房地产市场价格是衡量市场经济健康稳定发展的重要指标之一，受到各级各界开放商、投资人、购房者、政府部门、相关学者的广泛关注。因此，剖析房地产价格变动的因素，研究其内在联系，预测未来发展趋势，对宏观调控房价以稳定市场发展具有重要意义。

重庆作为最年轻的直辖市，自1998年废止住房分配制度后，通过住房公积金、住房贷款等金融手段跟随行业发展稳步进入房地产市场化阶段[1]。中国特色社会主义进入新时代，习近平总书记在十九大报告中指出要坚持“房子是用来住的，不是用来炒的”定位，加快建立房地产市场健康稳定发展长效机制[2]。在此背景下，重庆市房地产调控政策逐步收紧，着力打击投资投机性购房需求，构建多层次住房供应体系，深化土地、人口制度改革，助力房地产行业稳定长效机制的建立。

从价格需求理论可以得出，房地产市场价格受供给和需求两方面影响。而我国人多地少的国情意味着房地产市场必将受到需求侧人口因素的影响。当前，我国发展正面临低生育率、老龄化等人口发展问题，给经济可持续发展和社会稳定带来了前所未有的压力。中共中央政治局于2021年5月31日提出实施一对夫妻可以生育三个子女政策及配套支持措施，长期看有利于改善人口年龄结构，扩大新增劳动力供给，减轻老年人口抚养比，增加社会整体活力[3]。对房地产行业而言，人口结构变化将影响购房需求、基础设施配套等方方面面，进而引起房价的波动。因此，本文从人口结构角度，基于人口自然结构、人口社会结构、人口地域结构三方面选取相应指标，通过多因素回归分析法探讨人口结构变化对重庆房价的影响，并提出相应建议以期推动其房地产行业稳定发展。

2 文献综述

人口结构按照不同特征大致分为三类：人口自然结构、人口社会结构、人口地域结构。

（1）人口自然结构与房价。国内的相关研究起步较晚，但近年来越来越多的学者开始关注人口结构与房地产市场的关系。邹瑾等学者从结构性视角，利用面板协整检验证明了人口老龄化对房价波动存在长期影响，同时利用面板误差修正模型讨论了人口结构影响房价波动的区域差别、原因[4];王先柱等学者通过系统聚类和距离判别方法对我国31个省市房地产市场发展划分等级，探讨人口老龄化、出生率与房价之间的关系，依据相应面板数据开展实证研究得出总体上人口老龄化会抑制房价上涨，而出生率会助推房价上涨[5]。

（2）人口社会结构与房价。社会结构中与房地产市场相关的有居民收入、文化即受教育程度等。冯皓等学者认为教育资源在数量上和质量上的差异已经部分体现在房价上，教育的“资本化”确实存在[6];张慧慧等学者利用2006年～2012年中国城镇住户调查数据和地级市层面的房地产价格数据，研究高等教育升学率与房价上涨之间的关系，结果得出男性和女性接受高等教育概率的差距随着房地产价格升高而拉大[7];李萌等学者通过分析2002—2016年我国30个省份的面板数据， 构建模型探讨老龄抚养比、教育水平等因素对的住宅商品房价格的影响，得出教育水平的提高对抑制房价具有正向促进作用[8]。

（3）人口地域结构与房价。随着城市化进程地不断加快，地域变化主要体现在城乡之间。任行伟等学者通过人口城镇化与商品房价格之间的关系进行理论分析与实证研究，发现人口城镇化既直接影响房价，也会通过城镇居民收入作为中介间接影响房价[9];何鑫等学者通过地理加权回归法证明流动人口带来的住房需求是提高房价的关键因素，且是使房价波动呈空间异质性的主要因素[10]。

从文献研究的总体上来看，目前已有不少学者通过实证分析得出了人口结构变化对房价有不同层次的影响。本文在已有研究的基础上，以重庆市为例，利用2008年～2019年能代表人口结构三个方面的指标数据，通过多因素回归分析法探究人口结构变化与重庆房价之间的关系。

3 数据与模型

3.1 变量说明

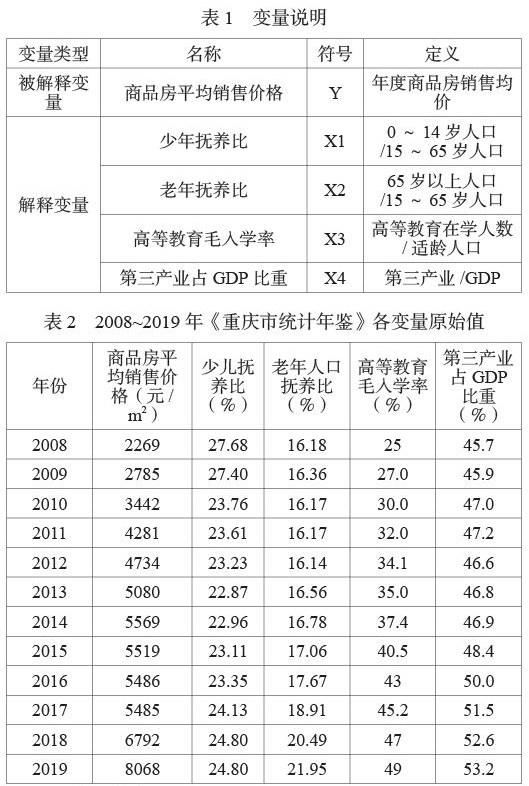
商品房平均销售价格为本研究中的因变量，用Y表示; 人口自然结构用少儿抚养比（X1） 、老年抚养比（X2） 表示; 人口社会结构采用地区高等教育毛入学率（X3） 表示，体现出研究区域整体文化素养水平; 关于人口地域结构，本文在此选取与城镇化水平有相互促进作用，是提升城镇化水平的持续动力的间接指标即第三产业，用第三产业占GDP比重（X4）表示。具体变量描述见表 1。

3.2 数据来源

本文选取 2008—2019 年重庆市的数据用于实证研究。其中，商品房平均销售价格、少年抚养比、老年抚养比、高等教育毛入学率、第三产业占GDP比重五个变量的数据均来自于《重庆市统计年鉴》，如表2所示。

3.3 模型构建

一个因变量与两个或更多的预测变量之间的联系被称为多元相关，在这种情况下做出的预测被称为多元回归[11]。本文为研究人口结构变化与房地产市场价格的关系，建立如下多元回归模型：

y=β0+β1X1+β2X2+β3X3+ε

其中Y为因變量;X为自变量;β是模型的参数;ε是均值为零，方差为σ2>0的不可观测的随机变量，称为误差项，并通常假定ε～N（0，σ2）。多元回归模型初步建立后，是否真正解释了预测变量和因变量的关系，还要进行显著性检验。