论文部分内容阅读
[摘要]目前,金融发展理论主要是从总量分析角度研究金融体系,本文参考了系统学关于无尺度网络的理论分析,提出金融系统是一个无尺度网络,具有强韧性和脆弱性的结构特性,并提出保持大型金融机构的财务稳健性,对保障我国金融系统清算和支付结算等主要功能实现具有重要意义。
[关键词]无尺度网络 复杂系统 金融体系
[中图分类号]F830 [文献标识码]A [文章编号]1004-6623(2007)02-0085-03
[作者简介]张韶辉(1972—),广东韶关人,注册金融分析师,南开大学经济学院博士研究生,供职于深圳市龙岗区发展和改革局。主要研究方向:金融发展理论。
一、引言
对金融体系进行系统研究,起始于戈德史密斯(Goldsmith.R.W)的《金融结构和金融发展》,他在该书中首次提出了衡量金融结构和金融发展水平的金融相关比率(FIR),即“某一时点上现存金融资产总额与国民财富之比”。通过对金融相关比率的分析,他得出的结论是:尽管不同国家的起点各不相同,但经济发展与金融发展之间存在着大致平行的关系。他还指出“金融结构越发达,金融工具和金融机构提供的选择机会就越多,资金总量的增加就越快,在一定的资金总量下,资金的使用效率就越高”。戈德史密斯对金融体系的研究,不仅利用金融相关比率进行总量分析,也提出了结构分析方法的重要性。而随后金融发展理论的研究脉络,更多的是仅沿着总量分析的框架开展,对金融体系结构问题的研究关注甚少。其间虽然有银行主导或市场主导的市场结构对比研究,但笔者认为,将银行主导与市场主导对立起来分析是一个误区,本质上两者间更多的是互补关系,而非竞争关系,都是金融体系结构多样化的必然要求。因此,本文主要借助系统学的研究成果,对金融体系的结构特征作初步的分析。
二、无尺度网络
系统学认为,元素、结构、环境三者共同决定系统的功能。设计具有特定功能的系统,须选择具有一定性能的元素,选择最佳的结构方案,还要创造适当的环境条件。系统结构是元素之间相对稳定的、有一定规则的联系方式的总和。按照结构性质分类,可以有空间结构和时间结构。元素在空间中的排列分布方式,称为空间结构,如晶体的点阵结构,建筑物的立体结构。系统运行过程中呈现出来的内在时间节律,如地球系统的周期运动、生物钟等,称为时间结构。系统的结构性对系统功能有着重要作用,例如同样或相近的元素,按不同结构组织起来,系统功能就有优劣高低之分,甚至会产生性质不同的功能。
(一)无尺度网络的定义。无尺度网络指的是网络节点的连结分布遵循“幂次定律”,即任何节点与其他k个节点相连结的概率,与l/kn成正比。以往科学家对复杂系统结构性问题的研究,一般认为复杂系统是一个随机网络,即系统中节点的连结方式是随机的,因此绝大部分节点的连结数目会大致相同,随机网络中节点的分布方式将遵循钟形的分布,连接数目比平均数高许多或低许多的节点都十分稀少。例如,1959年匈牙利数学家厄多斯(Erdos)和瑞尼(Renyi)提出通过在网络节点间随机地布置连结,就可以有效地模拟出通信和生命科学网络这类系统。1998年美国科学家阿尔伯特·拉兹洛·巴拉巴斯(Albert-Laszlo Barabasi)和埃里克·博纳博(Eric Bonabeau)在开展互联网项目研究初期,认为人们会根据自己的兴趣决定连结网络文件的网站,而个人兴趣的多样性和可选择的网页数量巨大,也假定互联网的连结模式将呈现出随机网络的特征。然而,研究结果却推翻了这个预测,事实上互联网是由少数高连结性的页面串连起来的,80%以上页面的连结数不到4个。然而只占节点总数不到万分之一的极少数节点,却有1000个以上的连结,也就是说网页的连结分布遵循“幂次定律”,任何节点与其他k个节点相连结的概率,与l/kn成正比,而且,n值通常介于2-3之间。幂次定律和表征随机网络的钟形分布大相径庭,幂次定律说明互联网是由少数集散节点所主控的系统。
随后的研究,也在很多不同的系统中发现了无尺度的系统结构特征。如以光纤或其他通信线路连接的路由器网络,电子邮件所连结的人际网络,物理和计算机等一些学科科学家之间的合作关系网络,美国生物技术产业的联盟网络,古菌域、细菌域和真核生物的细胞代谢网络。这些本质上不同的各种系统,却具有相同的结构特征,即不仅是无尺度的,而且有着一个共同点,系统节点的连结分布遵循的“幂次定律”中,kn项中的n值通常介于2~3之间。
(二)无尺度网络的特性。阿尔伯特和埃里克的研究认为,无尺度网络具有以下的特性:
1.网络成长性。无尺度网络的节点数量均呈现高增长现象,例如互联网的页面数量,1990年整个互联网只有一个网页,而到今天它的网页数已经是数以亿计,其它大部分网络也都具有类似的发展过程。互联网在起步阶段只有几个路由器,随着新的路由器与网络原有的路由器相连结,如今路由器的数量已经高达百万以上。这些现实中的无尺度网络,均具有不断快速成长的重要特性。
2.优先连结性。无尺度网络新增节点在连结过程中,并非所有旧节点的机会都是平等的,这种现象也称之为“马太效应”。例如,在选择将网页连结到何处时,尽管人们可以从数十亿个网站中进行选择,然而我们大部分人只熟悉整个互联网的一小部分,这一小部分往往就是那些拥有较多连结的站点,只要连结到这些站点,就等于基本联结了整个网络。这种“优先连结”的过程,也发生在其他网络。在互联网,那些连结较多的路由器通常拥有更大的带宽;在美国的生物技术产业,知名公司更容易吸引到同盟者的参与合作。
3.网络强韧性。研究中发现,无尺度复杂网络对随机的意外故障具有很强的承受能力。例如,路由器网络中每时每刻都有数百个路由器失效,但互联网却很少因此受到大的影响。模拟实验证明,即使从互联网路由器中随机选择的失效节点比例高达80%,剩余的路由器还是能组成一个完整的集群并保证任意两个节点间存在通路。研究认为,无尺度网络对随机性的意外故障具有强韧性的特征,本质上源于这些网络的非同质拓扑结构。随机去除方式所破坏的主要是那些不重要的节点,因为它们的数目远大于集散节点,因而去除它们不会对网络拓扑结构产生重大的影响。
4.网络脆弱性。无尺度网络过分依赖集散节点,使其面对主要集散节点的蓄意攻击时可能不堪一击。模拟试验发现,只要去除少数几个主要集散节点,就可导致互联网溃散成孤立无援的小群路由器。因此,一次有组织的协同攻击,只要去除掉若干个集散节点(先去除最大的,再去除次大的,依次类推),当有5%~10%的集散节点同时失效时,就足以造成无尺度网络的严重破坏。
三、金融体系与无尺度网络
金融体系是一个有关资金集中、流动、分配和再分配的系统。它由资金的流出方(资金盈余方)、流入方(资金短缺方)和连接这两者的金融中介机构与金融市场,以及对这三方进行管理的中央银行和其他金融监管机构共同组成。居民、企业、中介组织和政府机构都是金融系统的要素,他们在金融活动中相互作用和相互制约,形成了一個有机的系统。金融系统个体的种类主要有家庭、企业、政府、金融机构、中央银行等,其中有些个体的数量是很大的。如金融系统中的家庭数以百万、千万、亿计量的。如中国的人口有13亿,家庭的个数多达数亿。企业的个数随国家的大小不同,可以是万、十万、百万……金融机构类型也是多样化,如商业银行、保险公司、信托投资公司、证券公司等。
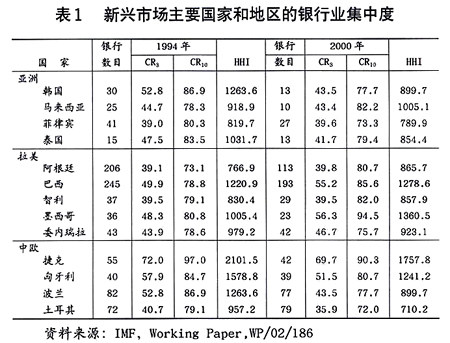
笔者认为,金融系统呈现出的结构特征,是一个无尺度网络,而不是一个随机网络系统。一方面,近年来包括中国在内的新兴市场主要国家和地区的金融体系,均呈现了快速增长态势。另一方面,一些大型金融机构作为金融体系中的集散节点,优先连结的特性十分明显。以国际货币基金组织关于新兴市场主要国家和地区的银行业集中度的研究为例,存款总额比重前3位和前10位的银行占市场份额平均约为50%和80%,也就是说,不论各新兴市场国家和地区具体情况如何不同,但在银行业发展和演化过程中,最终形成的市场结构均具有大致相同的结构特征,即存款总额比重前3位和前10位的银行占市场份额平均约为50%和80%,这充分说明了银行系统也是一个无尺度网络,大型银行机构在其中扮演着集散节点的角色。
事实上,如果将金融体系理解为一个无尺度网络,则个人、企业、金融机构等均是网络中的节点,个人和企业从数量上占网络中结点的绝大多数,但它们仅与网络中少数的金融机构相联系,因此是属于分散节点,而金融机构尽管仅占极少数,但它们却与网络中大多数节点相联系,因此属于无尺度网络中的集散节点。如果将金融机构单独作为一个子系统,也是一个无尺度网络,大型的金融机构扮演着集散节点角色,与大多数中小型金融机构发生资金业务往来,而中小型金融机构仅是与个别大型金融机构发生资金往来,并且是通过这些大型金融机构与其它金融机构间接发生联系。
如果将金融机构系统看成是经济系统中的一个子系统,经济系统中各行各业的兴衰均可能对金融系统造成冲击,假定各行各业的兴衰是独立于金融系统之外的随机性事件,则其对金融系统的冲击主要是一种随机性冲击,因此,金融系统作为经济系统的子系统,演化过程中形成的无尺度网络结构特征,与其在应对各行各业的兴衰过程中表现出的良好稳定性是相适应的。此外,默顿和博迪金提出,金融体系的主要功能是在一个不确定的环境中,帮助地区或国家之间配置和使用经济资源。金融系统的主要功能包括清算和支付结算,聚集和分配资源、在不同时间和不同空间之间转移资源。笔者认为,金融系统演化过程中形成的无尺度网络结构特征,有利于更好地实现清算和支付结算等主要功能,保持系统功能在外部随机性冲击下具有的强韧性。以清算和支付结算功能为例,金融系统中的各个节点,包括金融机构、企业和个人等,均不时受到各种各样的随机性外部冲击,许多节点的资金周转出现困难,甚至陷入财务危机,如果清算和支付结算网络是个随机网络,则该网络极有可能陷入瘫痪。但现实中,金融系统形成的无尺度网络结构特征,却保证了金融系统不会陷入瘫痪之中,其主要的清算和支付结算功能仍然可以维持。当然,金融系统作为一个无尺度网络也有脆弱性,当主要节点遭遇蓄意冲击,或者其自身机能不完善而陷入财务危机时,整个金融系统主要功能的实现将大打折扣。例如,东南亚金融危机中,外国对冲基金对其金融市场进行蓄意冲击,致使主要金融机构出现财务危机,造成了整个金融体系动荡不安,清算和支付结算等主要功能出现严重障碍,进而波及到经济实体各个部门。
四、结论与政策建议
阿尔伯特和埃里克认为,为了避免因恶意攻击带来网络的大规模破坏,最有效的办法就是保护好集散节点。笔者认为,考虑到无尺度网络具有的强韧性和脆弱性的双重特性,因此,保护好金融系统中集散节点对我国金融体系的发展意义重大。
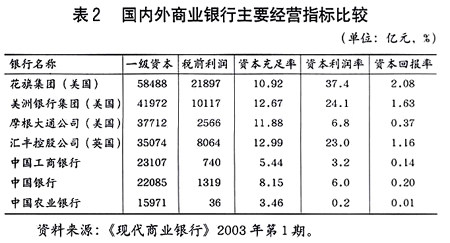
目前,我国金融系统存在的主要问题是大型金融机构作为系统的主要节点,在财务方面存在着极大隐忧,表2是国内外商业银行主要经营指标的比较。
资产规模位于前列的工商银行、中国银行、农业银行等大型金融机构,如果不能有效地改进其财务状况,一旦发生财务危机,其对我国金融系统造成的整体冲击将是巨大的。因此,笔者认为,近年来我国不惜采取一些非市场化手段,来弥补一些大型金融机构的潜在亏损,并通过海外上市方式引入战略投资者来强化内部市场化运行机制,有其合理性和必要性。只有完善和改进金融市场中资产规模位居前列的大型金融机构的财务稳健性,才能使我国金融系统清算和支付结算、聚集和分配资源、在不同时间和不同空间之间转移资源等主要功能得到保障,整个国民经济系统才不会出现陷入动荡之中。
[参考文献]
[1] Albert-Laszlo Barabasi 和Eric Bonabeau.无尺度网络[J].科学美国人中文版,2003,(7).
[2] 李幼平.无尺度现象引发的思考——文化传播对网络的反作用[DB].传媒投资网2005,(3).
[3] 唐芙蓉,蔡绍洪,李朝辉.无尺度网络中的统计力学特征[J].贵州大学学报,2005,(1).
[4] 刘青,刘寿强.无尺度网络在反蠕虫领域的应用[J].计算机安全,2005,(7).
[5] 曹黎.无尺度网络面临安全问题[J].IT时代周刊计算机安全,2004,(12/14).
[6] 吳家睿.生物系统的分子构建[J].科学,2006,(9).
[7] 陈关荣.复杂动力网络的研究将是新世纪科学技术前沿的战略性课题之一[Z].香港城市大学“混沌控制与同步”研究中心.
[关键词]无尺度网络 复杂系统 金融体系
[中图分类号]F830 [文献标识码]A [文章编号]1004-6623(2007)02-0085-03
[作者简介]张韶辉(1972—),广东韶关人,注册金融分析师,南开大学经济学院博士研究生,供职于深圳市龙岗区发展和改革局。主要研究方向:金融发展理论。
一、引言
对金融体系进行系统研究,起始于戈德史密斯(Goldsmith.R.W)的《金融结构和金融发展》,他在该书中首次提出了衡量金融结构和金融发展水平的金融相关比率(FIR),即“某一时点上现存金融资产总额与国民财富之比”。通过对金融相关比率的分析,他得出的结论是:尽管不同国家的起点各不相同,但经济发展与金融发展之间存在着大致平行的关系。他还指出“金融结构越发达,金融工具和金融机构提供的选择机会就越多,资金总量的增加就越快,在一定的资金总量下,资金的使用效率就越高”。戈德史密斯对金融体系的研究,不仅利用金融相关比率进行总量分析,也提出了结构分析方法的重要性。而随后金融发展理论的研究脉络,更多的是仅沿着总量分析的框架开展,对金融体系结构问题的研究关注甚少。其间虽然有银行主导或市场主导的市场结构对比研究,但笔者认为,将银行主导与市场主导对立起来分析是一个误区,本质上两者间更多的是互补关系,而非竞争关系,都是金融体系结构多样化的必然要求。因此,本文主要借助系统学的研究成果,对金融体系的结构特征作初步的分析。
二、无尺度网络
系统学认为,元素、结构、环境三者共同决定系统的功能。设计具有特定功能的系统,须选择具有一定性能的元素,选择最佳的结构方案,还要创造适当的环境条件。系统结构是元素之间相对稳定的、有一定规则的联系方式的总和。按照结构性质分类,可以有空间结构和时间结构。元素在空间中的排列分布方式,称为空间结构,如晶体的点阵结构,建筑物的立体结构。系统运行过程中呈现出来的内在时间节律,如地球系统的周期运动、生物钟等,称为时间结构。系统的结构性对系统功能有着重要作用,例如同样或相近的元素,按不同结构组织起来,系统功能就有优劣高低之分,甚至会产生性质不同的功能。
(一)无尺度网络的定义。无尺度网络指的是网络节点的连结分布遵循“幂次定律”,即任何节点与其他k个节点相连结的概率,与l/kn成正比。以往科学家对复杂系统结构性问题的研究,一般认为复杂系统是一个随机网络,即系统中节点的连结方式是随机的,因此绝大部分节点的连结数目会大致相同,随机网络中节点的分布方式将遵循钟形的分布,连接数目比平均数高许多或低许多的节点都十分稀少。例如,1959年匈牙利数学家厄多斯(Erdos)和瑞尼(Renyi)提出通过在网络节点间随机地布置连结,就可以有效地模拟出通信和生命科学网络这类系统。1998年美国科学家阿尔伯特·拉兹洛·巴拉巴斯(Albert-Laszlo Barabasi)和埃里克·博纳博(Eric Bonabeau)在开展互联网项目研究初期,认为人们会根据自己的兴趣决定连结网络文件的网站,而个人兴趣的多样性和可选择的网页数量巨大,也假定互联网的连结模式将呈现出随机网络的特征。然而,研究结果却推翻了这个预测,事实上互联网是由少数高连结性的页面串连起来的,80%以上页面的连结数不到4个。然而只占节点总数不到万分之一的极少数节点,却有1000个以上的连结,也就是说网页的连结分布遵循“幂次定律”,任何节点与其他k个节点相连结的概率,与l/kn成正比,而且,n值通常介于2-3之间。幂次定律和表征随机网络的钟形分布大相径庭,幂次定律说明互联网是由少数集散节点所主控的系统。
随后的研究,也在很多不同的系统中发现了无尺度的系统结构特征。如以光纤或其他通信线路连接的路由器网络,电子邮件所连结的人际网络,物理和计算机等一些学科科学家之间的合作关系网络,美国生物技术产业的联盟网络,古菌域、细菌域和真核生物的细胞代谢网络。这些本质上不同的各种系统,却具有相同的结构特征,即不仅是无尺度的,而且有着一个共同点,系统节点的连结分布遵循的“幂次定律”中,kn项中的n值通常介于2~3之间。
(二)无尺度网络的特性。阿尔伯特和埃里克的研究认为,无尺度网络具有以下的特性:
1.网络成长性。无尺度网络的节点数量均呈现高增长现象,例如互联网的页面数量,1990年整个互联网只有一个网页,而到今天它的网页数已经是数以亿计,其它大部分网络也都具有类似的发展过程。互联网在起步阶段只有几个路由器,随着新的路由器与网络原有的路由器相连结,如今路由器的数量已经高达百万以上。这些现实中的无尺度网络,均具有不断快速成长的重要特性。

2.优先连结性。无尺度网络新增节点在连结过程中,并非所有旧节点的机会都是平等的,这种现象也称之为“马太效应”。例如,在选择将网页连结到何处时,尽管人们可以从数十亿个网站中进行选择,然而我们大部分人只熟悉整个互联网的一小部分,这一小部分往往就是那些拥有较多连结的站点,只要连结到这些站点,就等于基本联结了整个网络。这种“优先连结”的过程,也发生在其他网络。在互联网,那些连结较多的路由器通常拥有更大的带宽;在美国的生物技术产业,知名公司更容易吸引到同盟者的参与合作。
3.网络强韧性。研究中发现,无尺度复杂网络对随机的意外故障具有很强的承受能力。例如,路由器网络中每时每刻都有数百个路由器失效,但互联网却很少因此受到大的影响。模拟实验证明,即使从互联网路由器中随机选择的失效节点比例高达80%,剩余的路由器还是能组成一个完整的集群并保证任意两个节点间存在通路。研究认为,无尺度网络对随机性的意外故障具有强韧性的特征,本质上源于这些网络的非同质拓扑结构。随机去除方式所破坏的主要是那些不重要的节点,因为它们的数目远大于集散节点,因而去除它们不会对网络拓扑结构产生重大的影响。
4.网络脆弱性。无尺度网络过分依赖集散节点,使其面对主要集散节点的蓄意攻击时可能不堪一击。模拟试验发现,只要去除少数几个主要集散节点,就可导致互联网溃散成孤立无援的小群路由器。因此,一次有组织的协同攻击,只要去除掉若干个集散节点(先去除最大的,再去除次大的,依次类推),当有5%~10%的集散节点同时失效时,就足以造成无尺度网络的严重破坏。
三、金融体系与无尺度网络
金融体系是一个有关资金集中、流动、分配和再分配的系统。它由资金的流出方(资金盈余方)、流入方(资金短缺方)和连接这两者的金融中介机构与金融市场,以及对这三方进行管理的中央银行和其他金融监管机构共同组成。居民、企业、中介组织和政府机构都是金融系统的要素,他们在金融活动中相互作用和相互制约,形成了一個有机的系统。金融系统个体的种类主要有家庭、企业、政府、金融机构、中央银行等,其中有些个体的数量是很大的。如金融系统中的家庭数以百万、千万、亿计量的。如中国的人口有13亿,家庭的个数多达数亿。企业的个数随国家的大小不同,可以是万、十万、百万……金融机构类型也是多样化,如商业银行、保险公司、信托投资公司、证券公司等。
笔者认为,金融系统呈现出的结构特征,是一个无尺度网络,而不是一个随机网络系统。一方面,近年来包括中国在内的新兴市场主要国家和地区的金融体系,均呈现了快速增长态势。另一方面,一些大型金融机构作为金融体系中的集散节点,优先连结的特性十分明显。以国际货币基金组织关于新兴市场主要国家和地区的银行业集中度的研究为例,存款总额比重前3位和前10位的银行占市场份额平均约为50%和80%,也就是说,不论各新兴市场国家和地区具体情况如何不同,但在银行业发展和演化过程中,最终形成的市场结构均具有大致相同的结构特征,即存款总额比重前3位和前10位的银行占市场份额平均约为50%和80%,这充分说明了银行系统也是一个无尺度网络,大型银行机构在其中扮演着集散节点的角色。
事实上,如果将金融体系理解为一个无尺度网络,则个人、企业、金融机构等均是网络中的节点,个人和企业从数量上占网络中结点的绝大多数,但它们仅与网络中少数的金融机构相联系,因此是属于分散节点,而金融机构尽管仅占极少数,但它们却与网络中大多数节点相联系,因此属于无尺度网络中的集散节点。如果将金融机构单独作为一个子系统,也是一个无尺度网络,大型的金融机构扮演着集散节点角色,与大多数中小型金融机构发生资金业务往来,而中小型金融机构仅是与个别大型金融机构发生资金往来,并且是通过这些大型金融机构与其它金融机构间接发生联系。
如果将金融机构系统看成是经济系统中的一个子系统,经济系统中各行各业的兴衰均可能对金融系统造成冲击,假定各行各业的兴衰是独立于金融系统之外的随机性事件,则其对金融系统的冲击主要是一种随机性冲击,因此,金融系统作为经济系统的子系统,演化过程中形成的无尺度网络结构特征,与其在应对各行各业的兴衰过程中表现出的良好稳定性是相适应的。此外,默顿和博迪金提出,金融体系的主要功能是在一个不确定的环境中,帮助地区或国家之间配置和使用经济资源。金融系统的主要功能包括清算和支付结算,聚集和分配资源、在不同时间和不同空间之间转移资源。笔者认为,金融系统演化过程中形成的无尺度网络结构特征,有利于更好地实现清算和支付结算等主要功能,保持系统功能在外部随机性冲击下具有的强韧性。以清算和支付结算功能为例,金融系统中的各个节点,包括金融机构、企业和个人等,均不时受到各种各样的随机性外部冲击,许多节点的资金周转出现困难,甚至陷入财务危机,如果清算和支付结算网络是个随机网络,则该网络极有可能陷入瘫痪。但现实中,金融系统形成的无尺度网络结构特征,却保证了金融系统不会陷入瘫痪之中,其主要的清算和支付结算功能仍然可以维持。当然,金融系统作为一个无尺度网络也有脆弱性,当主要节点遭遇蓄意冲击,或者其自身机能不完善而陷入财务危机时,整个金融系统主要功能的实现将大打折扣。例如,东南亚金融危机中,外国对冲基金对其金融市场进行蓄意冲击,致使主要金融机构出现财务危机,造成了整个金融体系动荡不安,清算和支付结算等主要功能出现严重障碍,进而波及到经济实体各个部门。
四、结论与政策建议
阿尔伯特和埃里克认为,为了避免因恶意攻击带来网络的大规模破坏,最有效的办法就是保护好集散节点。笔者认为,考虑到无尺度网络具有的强韧性和脆弱性的双重特性,因此,保护好金融系统中集散节点对我国金融体系的发展意义重大。

目前,我国金融系统存在的主要问题是大型金融机构作为系统的主要节点,在财务方面存在着极大隐忧,表2是国内外商业银行主要经营指标的比较。
资产规模位于前列的工商银行、中国银行、农业银行等大型金融机构,如果不能有效地改进其财务状况,一旦发生财务危机,其对我国金融系统造成的整体冲击将是巨大的。因此,笔者认为,近年来我国不惜采取一些非市场化手段,来弥补一些大型金融机构的潜在亏损,并通过海外上市方式引入战略投资者来强化内部市场化运行机制,有其合理性和必要性。只有完善和改进金融市场中资产规模位居前列的大型金融机构的财务稳健性,才能使我国金融系统清算和支付结算、聚集和分配资源、在不同时间和不同空间之间转移资源等主要功能得到保障,整个国民经济系统才不会出现陷入动荡之中。
[参考文献]
[1] Albert-Laszlo Barabasi 和Eric Bonabeau.无尺度网络[J].科学美国人中文版,2003,(7).
[2] 李幼平.无尺度现象引发的思考——文化传播对网络的反作用[DB].传媒投资网2005,(3).
[3] 唐芙蓉,蔡绍洪,李朝辉.无尺度网络中的统计力学特征[J].贵州大学学报,2005,(1).
[4] 刘青,刘寿强.无尺度网络在反蠕虫领域的应用[J].计算机安全,2005,(7).
[5] 曹黎.无尺度网络面临安全问题[J].IT时代周刊计算机安全,2004,(12/14).
[6] 吳家睿.生物系统的分子构建[J].科学,2006,(9).
[7] 陈关荣.复杂动力网络的研究将是新世纪科学技术前沿的战略性课题之一[Z].香港城市大学“混沌控制与同步”研究中心.