论文部分内容阅读
摘 要: 本文立足于学生数学基础薄弱和对《线性代数》的不同需求的现状,通过对现状进行调研和对历届学生做跟踪调查,深入分析目前《线性代数》教学中存在的主要问题和学生的考研意向,将分层教学模式引入该课程教学,通过相关抽样调查和对比分析等数理分析方法不断完善分层教学的层级和有效教学内容权重。
关键词:《线性代数》 分层教学模式 数理分析
《线性代数》课程是高等院校各专业培养计划中重要的公共基础理论课,其目的在于培养经济管理和工程技术人才所必备的数学素质,为培养我国现代化建设需要的高素质人才服务。在高等院校,《线性代数》的学习,不仅使学生的知识结构扩充,更重要的是对培养学生的创造性思维能力、抽象概括能力、逻辑推理能力、自学能力、分析问题和解决问题能力、对开阔学生思路,提高学生综合素质等都有很大帮助。因此,《线性代数》的教学一直深受重视并且不断提出高要求。通过基于学生考研的《线性代数》分层教学模式的探索和研究,尽可能做到对有考研意向的同学和其他学生之间的和谐共处,既有利于学生考研目标的实现,又有利于提高整体的教学质量。
1.研究背景
自1999年实行普通高等学校扩招政策后,各高校均面临着学生规模迅速扩大,地区性教育质量的不同导致学生素质参差不齐,生源总体差异显著加大,按总分录取的方式使单科成绩差距悬殊的现象存在;另外,近年来,在巨大的就业压力面前,很多学生把考研作为第一选择,而《线性代数》作为大多数专业考研的必考课程之一,虽然所占分值不高,但属于必须全取的分数,因而该课程教学质量,也直接影响学生的备考。在这种情形下,若仍采用传统的教学模式,为任课教师有效组织教学等带来极大的困难,对提高教学质量极为不利。鉴于上述种种原因,改革传统的教学模式势在必行。本文的创新之处在于将对学生的基本要求和对学生考研的特殊要求融为一体,让学生各取所需,按需完成课程学习。分层教学模式将在部分班级进行试点教学,待时机成熟推广至全院所有班级,并将其经验分享到《高等数学》等其他数学类课程的教学中。
2.研究内容
线性代数是19世纪后期发展起来的一个数学分支,它是高等院校理工科各专业及经济管理等专业的一门基础必修课,也是硕士研究生入学考试数学科目的一部分。它是为培养我国社会主义现代化建设所需要的高质量专门人才服务的。本课程主要讨论有限维线性空间的线性理论与方法,具有较强的逻辑性、抽象性与广泛的实用性。线性代数这一数学工具在经济、管理科学中有着广泛的应用,著名的投入产出模型就是以线性代数理论为基础的。学好这门课程不仅对学习后继课程是必不可少,而且对掌握现代经济理论应用是非常必要的。尤其在计算机日益普及的今天,解大型线性方程组,求矩阵的特征值等已经成为技术人员经常遇到的课题。因此,本课程所介绍的方法广泛应用于各个学科。
通过本课程的学习,学生获得应用科学中常用的矩阵方法,线性方程组、二次型等理论及其有关的基础知识,培养学生的抽象思维能力、逻辑推理能力、熟练运算能力,并具有熟练的矩阵运算能力和用矩阵方法解决一些实际问题的能力,从而为学习后继课程及进一步扩大数学知识面,提高学生素质奠定必要的基础。
以往,我院该课程在不同专业的开课时间和课程学时安排不一致,工科专业每周2学时,理科专业每周3学时,经济类每周4学时,但在考研中理工科对线性代数的要求难度大于经济类,在教学过程中往往呈现出理工类课时不够,进度较赶,学生学习结果不够理想的结果。
本文主要是根据现行学生学习现状及历年考研学生的跟踪调查,考研学生的需求,对该课程教学过程中存在的问题进行分析解决。首先是重新制定教学大纲,使每个专业保证课时量。再借鉴高数和概率论尖子班的模式,拟开办线性代数尖子班,将分层教学理念引入,既保证全体学生学习线性代数这门课程的基本需求,又力使有考研需求的学生提高线性代数解题能力,还最大限度地完善课后练习题题库和考研真题题库。
3.研究的方法及步骤
基于学生考研的《线性代数》课程分层教学模式探索与研究课题申报成功以后,本课题组各成员积极搜集资料,调查分析,以便于分层教学模式的开展。现将完成的工作作以下概述。
(1)基本知识:掌握行列式的计算,矩阵的各种运算及其运算律,利用矩阵的初等变换求矩阵的秩、解线性方程组、判别向量组的线性相关性及求极大无关组,利用正交矩阵化对称矩阵为对角阵等基础知识。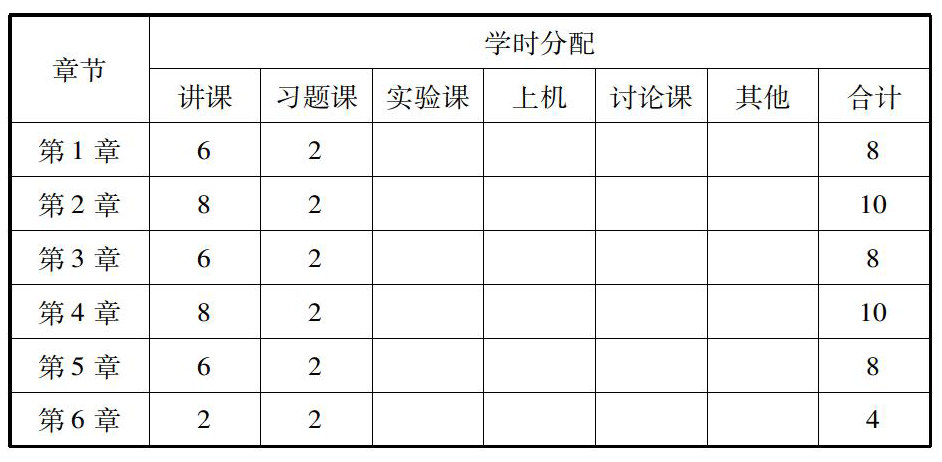
(2)基本能力:培养学生抽象思维能力、逻辑推理能力、基本运算能力、自学能力与科学创新能力及用线性代数方法分析和解决实际问题的能力。
(3)基本技能:使学生具有矩阵运算、利用矩阵方法解决一些实际问题、数学建模及用数学软件进行分析解决实际问题的能力。
(4)课程教学基本要求:在课堂讲授中要重点对基本概念、基本方法和解题思路的讲解。采用启发式教学。重要定理、例题要以黑板书写为主,抽象概念要尽量通过多媒体直观演示,以确保在有限学时内,全面高质量完成课程教学任务。在课堂讲授中,可增加问题的讨论环节,调动学生学习的主观能动性,注意培养学生解决实际问题的能力。如果条件允许,可以安排一定学时的数学实验课,用matlab语言进行繁琐的运算。
(5)作业:采用练习册,每章习题必做。定期收取学生作业,至少批改任课班级学生总数的三分之一,并且每次给出作业成绩,可按A,B,C等分类。
(6)成绩考核:最后总评成绩按期终考试成绩占80%,平时成绩(包括出勤、作业、回答问题等)占20%计算。
(7)学时分配:
本文拟解决的主要问题,如何对学生进行分层并运用分层教学的方法使有考研意向学生和其他同时受益,在调动学生学习积极性和从整体上提高教学质量的基础上,尽量让有考研意向的学生更好地朝着考研目标迈进。
参考文献:
[1]胡清洁,陈玉.浅谈改进线性代数课堂教学的几点做法[J].教育教学论坛,2015(13).
[2]原江涛,王彩虹.关于线性代数教学有效性的探索[J].科教文汇(上旬刊),2014(05).
[3]房剑平.线性代数课堂教学的几点体会[J].考试周刊,2014(18).
[4]王颖,南基洙.线性代数教学中的归纳与演绎方法[J].高等数学研究,2013(06).
[5]成琨,任永泰.提高线性代数课堂教学有效性方法的探讨[J].大学教育,2013(10).
[6]赵俊芳,陈旭东,廉海荣.关于“线性代数”课程教学改革的几点思考[J].中国地质教育,2012(02).
关键词:《线性代数》 分层教学模式 数理分析
《线性代数》课程是高等院校各专业培养计划中重要的公共基础理论课,其目的在于培养经济管理和工程技术人才所必备的数学素质,为培养我国现代化建设需要的高素质人才服务。在高等院校,《线性代数》的学习,不仅使学生的知识结构扩充,更重要的是对培养学生的创造性思维能力、抽象概括能力、逻辑推理能力、自学能力、分析问题和解决问题能力、对开阔学生思路,提高学生综合素质等都有很大帮助。因此,《线性代数》的教学一直深受重视并且不断提出高要求。通过基于学生考研的《线性代数》分层教学模式的探索和研究,尽可能做到对有考研意向的同学和其他学生之间的和谐共处,既有利于学生考研目标的实现,又有利于提高整体的教学质量。
1.研究背景
自1999年实行普通高等学校扩招政策后,各高校均面临着学生规模迅速扩大,地区性教育质量的不同导致学生素质参差不齐,生源总体差异显著加大,按总分录取的方式使单科成绩差距悬殊的现象存在;另外,近年来,在巨大的就业压力面前,很多学生把考研作为第一选择,而《线性代数》作为大多数专业考研的必考课程之一,虽然所占分值不高,但属于必须全取的分数,因而该课程教学质量,也直接影响学生的备考。在这种情形下,若仍采用传统的教学模式,为任课教师有效组织教学等带来极大的困难,对提高教学质量极为不利。鉴于上述种种原因,改革传统的教学模式势在必行。本文的创新之处在于将对学生的基本要求和对学生考研的特殊要求融为一体,让学生各取所需,按需完成课程学习。分层教学模式将在部分班级进行试点教学,待时机成熟推广至全院所有班级,并将其经验分享到《高等数学》等其他数学类课程的教学中。
2.研究内容
线性代数是19世纪后期发展起来的一个数学分支,它是高等院校理工科各专业及经济管理等专业的一门基础必修课,也是硕士研究生入学考试数学科目的一部分。它是为培养我国社会主义现代化建设所需要的高质量专门人才服务的。本课程主要讨论有限维线性空间的线性理论与方法,具有较强的逻辑性、抽象性与广泛的实用性。线性代数这一数学工具在经济、管理科学中有着广泛的应用,著名的投入产出模型就是以线性代数理论为基础的。学好这门课程不仅对学习后继课程是必不可少,而且对掌握现代经济理论应用是非常必要的。尤其在计算机日益普及的今天,解大型线性方程组,求矩阵的特征值等已经成为技术人员经常遇到的课题。因此,本课程所介绍的方法广泛应用于各个学科。
通过本课程的学习,学生获得应用科学中常用的矩阵方法,线性方程组、二次型等理论及其有关的基础知识,培养学生的抽象思维能力、逻辑推理能力、熟练运算能力,并具有熟练的矩阵运算能力和用矩阵方法解决一些实际问题的能力,从而为学习后继课程及进一步扩大数学知识面,提高学生素质奠定必要的基础。
以往,我院该课程在不同专业的开课时间和课程学时安排不一致,工科专业每周2学时,理科专业每周3学时,经济类每周4学时,但在考研中理工科对线性代数的要求难度大于经济类,在教学过程中往往呈现出理工类课时不够,进度较赶,学生学习结果不够理想的结果。
本文主要是根据现行学生学习现状及历年考研学生的跟踪调查,考研学生的需求,对该课程教学过程中存在的问题进行分析解决。首先是重新制定教学大纲,使每个专业保证课时量。再借鉴高数和概率论尖子班的模式,拟开办线性代数尖子班,将分层教学理念引入,既保证全体学生学习线性代数这门课程的基本需求,又力使有考研需求的学生提高线性代数解题能力,还最大限度地完善课后练习题题库和考研真题题库。
3.研究的方法及步骤
基于学生考研的《线性代数》课程分层教学模式探索与研究课题申报成功以后,本课题组各成员积极搜集资料,调查分析,以便于分层教学模式的开展。现将完成的工作作以下概述。
(1)基本知识:掌握行列式的计算,矩阵的各种运算及其运算律,利用矩阵的初等变换求矩阵的秩、解线性方程组、判别向量组的线性相关性及求极大无关组,利用正交矩阵化对称矩阵为对角阵等基础知识。

(2)基本能力:培养学生抽象思维能力、逻辑推理能力、基本运算能力、自学能力与科学创新能力及用线性代数方法分析和解决实际问题的能力。
(3)基本技能:使学生具有矩阵运算、利用矩阵方法解决一些实际问题、数学建模及用数学软件进行分析解决实际问题的能力。
(4)课程教学基本要求:在课堂讲授中要重点对基本概念、基本方法和解题思路的讲解。采用启发式教学。重要定理、例题要以黑板书写为主,抽象概念要尽量通过多媒体直观演示,以确保在有限学时内,全面高质量完成课程教学任务。在课堂讲授中,可增加问题的讨论环节,调动学生学习的主观能动性,注意培养学生解决实际问题的能力。如果条件允许,可以安排一定学时的数学实验课,用matlab语言进行繁琐的运算。
(5)作业:采用练习册,每章习题必做。定期收取学生作业,至少批改任课班级学生总数的三分之一,并且每次给出作业成绩,可按A,B,C等分类。
(6)成绩考核:最后总评成绩按期终考试成绩占80%,平时成绩(包括出勤、作业、回答问题等)占20%计算。
(7)学时分配:
本文拟解决的主要问题,如何对学生进行分层并运用分层教学的方法使有考研意向学生和其他同时受益,在调动学生学习积极性和从整体上提高教学质量的基础上,尽量让有考研意向的学生更好地朝着考研目标迈进。
参考文献:
[1]胡清洁,陈玉.浅谈改进线性代数课堂教学的几点做法[J].教育教学论坛,2015(13).
[2]原江涛,王彩虹.关于线性代数教学有效性的探索[J].科教文汇(上旬刊),2014(05).
[3]房剑平.线性代数课堂教学的几点体会[J].考试周刊,2014(18).
[4]王颖,南基洙.线性代数教学中的归纳与演绎方法[J].高等数学研究,2013(06).
[5]成琨,任永泰.提高线性代数课堂教学有效性方法的探讨[J].大学教育,2013(10).
[6]赵俊芳,陈旭东,廉海荣.关于“线性代数”课程教学改革的几点思考[J].中国地质教育,2012(02).